Project

Algorithms & Data Structures

Three algorithmic implementations developed as part of an Algorithms and Data Structures course, each addressing a different fundamental problem through rigorous design, implementation, and complexity analysis.

Together, the three projects form a cohesive exploration of classical data structures and graph-based algorithms, with a strong emphasis on correctness, efficiency, and formal reasoning.

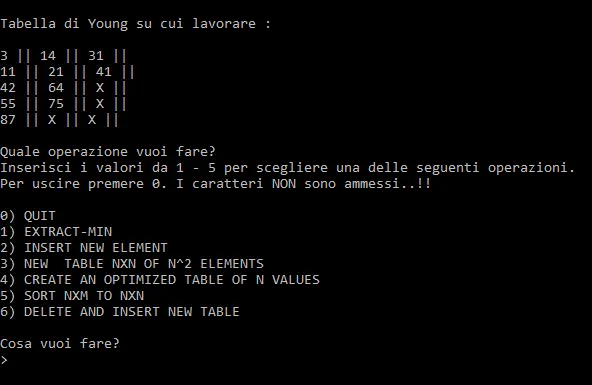
The first project focuses on the design and implementation of the Young Tableau data structure, a two-dimensional matrix in which elements are ordered both row-wise and column-wise. The implementation supports a wide range of operations, including tableau creation, insertion of new values, extraction of the minimum element, and transformation between different tableau dimensions. Special attention is given to preserving the structural properties of the Young Tableau through heap-based reordering strategies. The project also includes procedures for dynamically adapting the tableau size based on the number of stored elements, along with a detailed analysis of best- and worst-case computational complexity.

The second project addresses the creation and management of Binary Search Trees (BSTs), providing a comprehensive set of operations such as node insertion, deletion, tree rotation, balancing, and merging of multiple trees. Beyond basic manipulation, the project explores the statistical behavior of BSTs by studying the average height of randomly generated trees as their size increases. This experimental analysis highlights theoretical properties of binary trees and illustrates how tree height converges within predictable bounds. The implementation also includes graphical tree visualization, reinforcing understanding of structural transformations and balancing strategies.

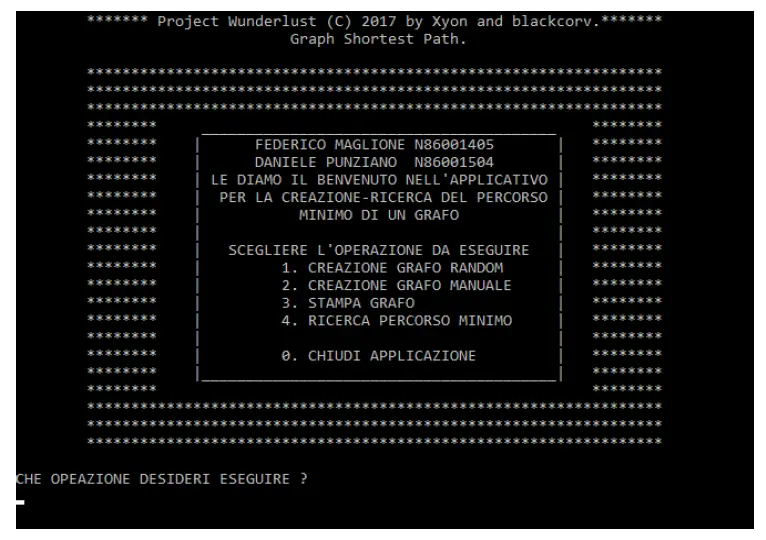
The third project applies graph theory and algorithmic optimization to solve a constrained shortest-path problem, modeled as a directed acyclic graph. The problem introduces additional constraints based on node elevation, requiring paths that first ascend and then descend. To efficiently compute the optimal solution, the project combines depth-first search for topological sorting with a linear-time shortest-path algorithm. Custom data structures are used to track distances, elevation transitions, and predecessor relationships, enabling reconstruction of the valid shortest path while maintaining optimal time complexity.